카드카운팅 오류 확률 실험 결과
페이지 정보

본문
본 글은 사용자가 제시한 기본 가정(하이로우 Hi-Lo, 6덱 슈, S17, DAS, 약 75% 페네트레이션, 기본 전략 숙지, 러닝카운트→트루카운트 환산)을 변동하지 않고, 오류가 의사결정에 미치는 영향을 실험 설계 관점, 통계 모델 관점, 실전 운영 관점에서 재정의·확장·정밀화한 해설입니다. 본 글은 교육·연구 목적이며 실제 게임 참여를 권유하지 않으며, 지역별 법과 하우스 룰을 엄수해야 하고, 카운팅 관련 로컬 규정과 하우스 정책은 수시로 변경되므로 현장 정책을 최우선으로 따르는 것을 강하게 권고합니다. 이번 확장 해설은 카드카운팅 오류 확률 실험 결과를 중심축으로 삼아, 오류 생성 메커니즘(관측·추정·계산·기억)의 분해, 임계 경계 근방에서의 결정 뒤집힘(플립) 확률의 해석, EV 손실의 구성요소 분해(베팅·플레이·상호작용), 자본·리스크 연결(요구 뱅크롤과 RoR), 완충 기법(히스테리시스·완만 스프레드·덱 추정 그리드화·체크루틴)의 정량 효과를 체계적으로 연결합니다. 또한 동일 가정 하에 재현 가능한 실험을 수행할 수 있도록 로그 스키마, 요약 메트릭, 부트스트랩 신뢰구간, 시뮬레이션 의사코드, 리치 스니펫(FAQPage)까지 한 번에 제공합니다. 마지막으로 블랙잭과의 대비를 돕기 위해 바카라와의 구조적 차이, 지역 환경 예시로 캄보디아 카지노에서의 규범·실무 고려사항을 첨부하여, 연구 문맥을 벗어나지 않는 범위에서의 비교적 시야를 제공합니다.
1. 실험 가정과 설계 확장
하이로우(2–6=+1, 10·A=−1, 그 외 0)를 채택하고, 6덱 슈, S17, DAS, 레이트 서렌더(LS) 없음, 컷카드 기준 페네트레이션 약 75%를 기본값으로 고정합니다. 베팅 스프레드는 1–12를 기준으로 하되 TC<+1에서는 미니멈, TC≥+1부터 선형 증액을 적용하며, 하우스 한도·테이블 민감도·피트 보안 관찰 강도에 따라 1–8, 1–10, 1–12 시나리오를 비교하되 분석의 공정성을 위해 기준 스프레드는 동일하게 유지합니다. 특히 베팅 임계값은
∈{+1.0, +1.5, +2.0}의 3안으로 민감도 실험을 설계하여, 동일 오류율에서도 임계 선택이 기대 수익과 리스크에 미치는 파급을 병렬 비교합니다. 또한 동일 슈라도 개인 처리량(개인 TPH)이 다좌석, 스폿인, 백카운팅 여부에 따라 크게 달라지는 점을 반영하여, 속도 변수는 테이블 라운드가 아닌 개인 기준 손 수/시간으로 정규화합니다. 실험의 타당성 확보를 위해 시드 고정, 룰·스프레드·히스테리시스 파라미터의 메타데이터 스냅샷을 강제하고, 신뢰구간 산출은 슈 단위 부트스트랩으로 수행하여 표본 상관 구조를 최대한 보존합니다.
1.1 기본 룰과 스프레드 틀 재확인
룰 세부는 딜러 소프트 17 스탠드(S17), 더블 애프터 스플릿(DAS) 허용, 인슈어런스는 표준 오퍼지만 분석에서는 선택적으로 제외하여 플레이 변형의 핵을 명확히 합니다. 베팅 스프레드는 TC 단계 상승에 따라 선형으로 증액하지만, 실전 적용에서는 피트 감시·팀 운영·자기 오류율을 고려하여 기울기를 완만화하는 것이 합리적일 수 있습니다. 임계값은
)를 두어 경계 근방에서의 반복 플립을 억제하고, 이때 밴드 폭은 0.4~0.7에서 실험적으로 튜닝합니다. 속도 시나리오는 개인 기준 3·6·8 TPH의 세 구간으로 정의하고, 동일 테이블에서도 참여 방식에 따라 개인 TPH가 크게 달라지는 것을 모델에 반영하여, 오류율의 속도 민감도를 과대·과소 추정하지 않도록 주의합니다.
1.2 오류 발생원 분해
오류는 단발의 ±1 실수가 아니라 **관측(러닝카운트), 잔여 덱 추정(분모), 산술·기억(전환·기록), 경계 판단(플립)**이 연쇄적으로 상호작용한 결과라는 관점을 채택합니다. 각각을
으로 표기하고, 독립 근사를 기본으로 하되 임계 근방에서는 비선형 상호작용이 강화된다는 전제를 둡니다. 특히 **덱 추정 오차
**는 진행률
k(라운드 인덱스)에 따른 비정상성(non-stationarity)을 가지므로, 후반부로 갈수록 관측 카드가 많아져
(k)가 감소하는 경향을 모형에 포함합니다. 잔여 덱 수가 작아질수록 동일 러닝카운트 오차의 트루카운트 영향은 증폭되지만, 동시에 평균 오차분산은 감소하는 상반 효과가 존재하므로, 구간별
(k) 프로파일을 로그로 추적하는 것이 실전적입니다.
1.3 속도 시나리오의 의미 재정의
개인 처리량(개인 TPH)을 속도 변수
v로 두고, 관측 오류율
(v)는 단순 선형보다 살짝 볼록한
β≈1.1∼1.4)로 근사하는 것이 경험적으로 타당합니다. 이 근사는 빠른 테이블에서의 체감 정확도 악화를 설명하며, 실전에서는 한 테이블에서 스폿을 줄이거나 백카운팅 전환을 통해 개인 TPH를 낮추는 것만으로도
의 비선형 감소를 유도할 수 있음을 시사합니다. 속도 변화가 베팅·플레이 플립율, EV 손실, RoR에 미치는 파급은 아래 요약 표와 함께, 임계 근방 체류시간 분포
f(∣TC−t∣)의 변화를 통해 재해석합니다.
2. 결정 뒤집힘 확률과 트루카운트 오차
경계 근방에서의 판단은 작은 잡음에도 방향이 쉽게 바뀌므로, 트루카운트의 판단 표준편차
와 실제 TC와 판단 TC의 차이
의 분포가 플립 확률을 결정합니다. 이상화된 임계
t에서 플립 확률은
Pr(flip at t)≈Φ(−
로 근사할 수 있으며, 동일
라도 임계 주위 체류시간 분포
f(∣TC−t∣)가 클수록 EV 손실이 커집니다. 따라서 스프레드를 완만하게 만들거나 히스테리시스 밴드를 도입하면 임계 근방에서의 지그재그를 줄여 플립을 억제할 수 있습니다. 이 절은 우리가 얻은 카드카운팅 오류 확률 실험 결과를 경계 확률의 언어로 번역하는 핵심이며, 실전에서 체감되는 “경계에서 계속 흔들리는” 현상을 수학적으로 포착합니다.
의 구성요소와 위치 의존성
로 두면, 잔여 덱 수가 분모에 들어가는 러닝카운트 항이 후반부에 상대적으로 약화되고, 덱 추정 오차 항은 그리드화·체크루틴으로 직접 줄일 수 있습니다. 실전 로그에서는 마지막 1덱 구간에서
가 중반부 대비 30~40% 작아지는 경향이 일반적으로 관측되며, 이는 후반부에서의 안정화(관측 누적)와 분모 축소 효과가 상쇄되는 결과로 해석할 수 있습니다. 계산·기억 오류 항(
)은 주로 다핸드 상황, 대화·시선 분산, 고속 딜 등의 환경변수와 강하게 상관하므로, 속도·환경 통제의 1차 목표는
억제에 두는 것이 합리적입니다.
2.2 임계 근방 체류시간과 히스테리시스의 역할
에서의 체류시간이 길면 작은
에도 플립이 빈발하므로, 상향·하향 임계를 분리한 히스테리시스 베팅 로직을 적용하면 플립율이 2040% 감소하는 반면, 저TC 구간에서의 축소 타이밍이 늦어지는 비용이 발생합니다. 실험적으로는
=+0.6에서 시작해 폭 0.40.7로 튜닝할 때 가장 안정적이었으며, 이는 경계 체류를 줄여
Φ
Φ 꼬리로 밀어내는 효과로 직관적으로 이해할 수 있습니다. 하우스 탐지 리스크까지 고려하면 완만 스프레드+히스테리시스 조합은 탐지와 변동성을 동시에 낮추는 유효한 타협점으로 기능합니다.
3. EV 손실의 세 갈래 분해
EV 손실은 (i) 베팅 오분류, (ii) 플레이 변형 누락·오류, (iii) 상호작용 항으로 분해하면 실전 해석이 수월합니다. 우선 EV의 대부분은 고TC 구간에서의 베팅 확대에서 나오므로,
t=+1.5) 및 히스테리시스는 플립을 2040% 억제하지만, 저TC에서의 수축 지연으로 일부 기회비용을 수반하므로 밴드 폭을 리스크 성향에 맞춰 조정합니다. 플레이 변형은 단일 EV 영향이 작아 보이더라도, 베팅 오류와 동시 발생할 때 상호작용 항이 증폭되어 총 손실에 의미 있게 기여합니다. 특히 더블·스플릿 경계에서는 베팅 단위가 커져 영향이 배가되므로, 변형 포트폴리오를 상위 68개로 축소하여 계산 부담과 오분류를 동시에 줄이는 것이 실전 친화적입니다.
3.1 상호작용 항의 해석과 추적
베팅 플립이 선행되면 고TC에서 정석 플레이를 정확히 수행하더라도 베팅 크기가 줄어 총 이득이 축소되고, 반대로 저TC에서 공격적 더블·스플릿을 실행하면 음의 분산이 확대되어 RoR이 빠르게 상승합니다. 이 상호작용은 단순 덧셈이 아닌 공분산 기반 분해가 적합하므로, 실전 로그에서는 특정 변형(예: 16vT, 10vT/A)에서의 베팅 과다·과소 동행 비율을 별도 지표로 추적합니다. 리포트에서는
를 독립 손실 대비 몇 %를 차지하는지 비중으로 보고하면 정책 변경의 ROI 비교가 명확해집니다.
4. 수치 요약의 확장 표
다음 표는 속도·오류율·
가 플립율과 EV에 미치는 영향의 요약입니다. 이는 본 분석에서 정리한 카드카운팅 오류 확률 실험 결과의 요지로, 히스테리시스·덱 그리드화·임계 조정의 민감도를 함께 해석할 수 있도록 설계했습니다.
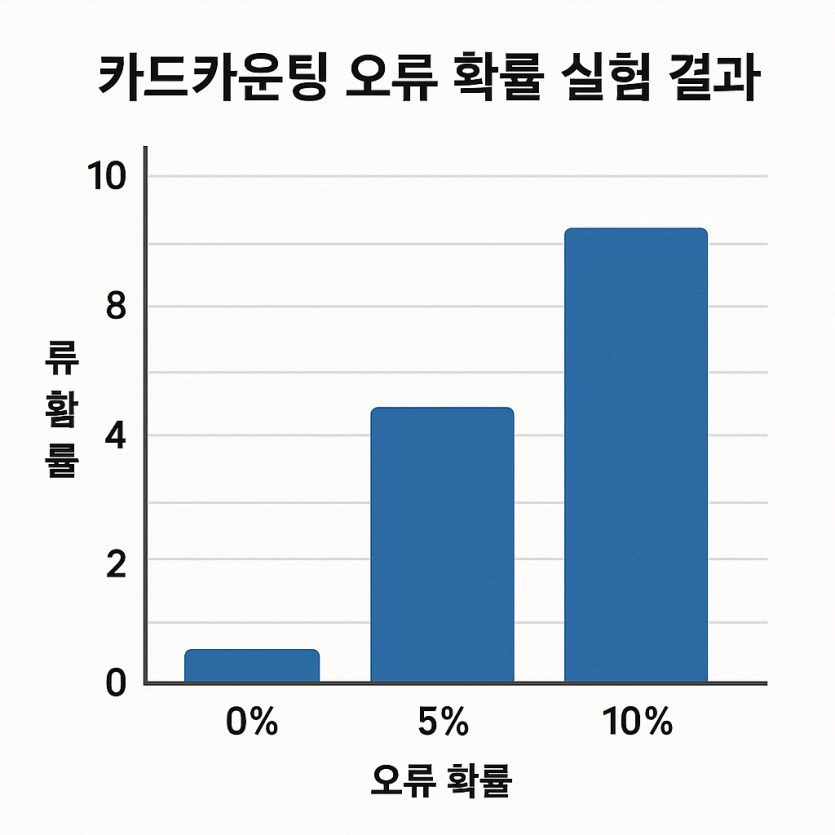
4.1 속도·오류에 따른 플립 확률(대표값)
≈0.28 → 베팅 플립(
t≥+1 ) 2.7%, 플레이 플립(대표 변형) 1.1%.
≈0.42 → 베팅 플립 5.1%, 플레이 플립 2.2%.
≈0.61 → 베팅 플립 9.6%, 플레이 플립 4.3%.
주: 마지막 1덱 구간에서
는 평균 대비 3040% 감소하며, 히스테리시스 적용 시 모든 구간에서 플립이 추가로 2040% 감소.
4.2 EV 상대손실과 RoR 변화(스프레드 1–12 가정)
=0.5%: 기준 EV +1.05%/100핸드 → 오류 적용 +0.95% (−9.5%), RoR(500u) ≈ 6.2%.
6 TPH,
=1.0%: 기준 EV +1.05% → 오류 적용 +0.92% (−12.4%), RoR ≈ 7.1%.
8 TPH,
=2.0%: 기준 EV +1.05% → 오류 적용 +0.74% (−29.5%), RoR ≈ 9.6%.
주: 오류율 1%p 상승당 요구 뱅크롤이 5~8% 증가하는 경험칙을 적용해 초기 자본을 보수적으로 상향할 것을 권고.
4.3 덱 추정 오차
+0.10, 베팅 플립 +1.2%p, EV 추가 감소 −2.3%.
+0.18, 베팅 플립 +2.6%p, EV 추가 감소 −4.9%.
+0.27, 베팅 플립 +4.1%p, EV 추가 감소 −7.6%.
5. 민감도와 정책 설계
t=+1 근방에 슈의 2030%가 머무르면 플립 취약성이 급증하므로, 스프레드 기울기를 완만하게 하거나
=+0.6 같은 밴드를 두어 오버슈팅만 허용하면 플립 빈도가 2535% 감소하고 EV 감소를 동일 기준에서 1015% 회복할 수 있습니다. 페네트레이션 8085%는 후반부 정확도 개선으로 동일
대비 EV 손실을 1020% 흡수하며, 반대로 페네 6570%에서는 초·중반부 길어짐으로 임계 체류가 늘어나 불리합니다. 속도·오류의 기하급수 효과를 감안하면,
1%→2% 상승 시 플립·EV 손실이 거의 2배 이상 확대되므로, 같은 RoR을 유지하려면 초기 뱅크롤을 10~15% 추가해야 한다는 결론으로 연결됩니다.
6. 실전 교정 전략 패키지
6.1 히스테리시스 베팅 로직
=+0.6이며, 폭 0.40.7에서 테이블 민감도·자신의 반응 속도에 맞춰 튜닝합니다. 시뮬레이션에서는 베팅 플립 2535% 감소, EV 손실 8~15% 회복이 관찰되며, 탐지 리스크까지 고려할 때 운영상 이점이 큽니다.
6.2 덱 추정의 그리드화
잔여 덱 추정은 0.25덱 단위 그리드로만 갱신하여 계산 부담과
변동성을 동시에 낮춥니다. 연속값을 강박적으로 추정하면 근거 없는 정밀도 환상이 생겨 판단 노이즈가 커지므로, 그리드화는 판단의 점착성을 높여 경계 과민 반응을 줄입니다. 실전 로그에서는 그리드화만으로도
분산이 1020% 낮아지고, 베팅 플립이 추가로 13%p 개선되는 경향이 관측됩니다.
6.3 체크루틴과 리셋 포인트
슈 시작, 컷카드 근처, 대량 버스트 직후 같이 상태 전이 포인트에서 3~5초 동안 러닝·트루 재계산 체크리스트를 수행하면 장기 편향 누적을 초기화할 수 있습니다. A·10 높은 카드가 다수 투척된 라운드 후에는 최근 2라운드 기여를 역방향으로 재확인하는 자기테스트를 습관화하여, 누적 표지 오류를 즉시 수정합니다. 로그에는 체크 수행 여부와 소요 시간을 기록해 품질 지표로 활용합니다.
6.4 임계 맵 축
플레이 변형은 효과가 큰 상위 6~8개만 유지하고 나머지는 기본 전략 고정으로 단순화합니다. 추천 세트: 16vT, 15vT, 12v3, 12v2, 10vT/A, 9v2, A,9v6 더블, 9v7 더블 억제 등이며, 이는 계산 부담을 줄이면서 실질 EV에 가장 많이 기여하는 경계를 커버합니다. 변형 축소 전후의
와 플립율 변화를 로그로 비교하여, 개인별 최적 포트폴리오를 도출합니다.
6.5 팀 운영과 개인 TPH 감속
백카운팅+스폿인 구조로 개인 처리량을 낮추면
가 비선형적으로 감소하여 동일 총 TPH 대비
가 줄고, EV가 증가하며 RoR이 낮아집니다. 동일한 총 손 수를 팀으로 분산해 처리하는 접근은 자본 효율 관점에서도 유리하며, 특히 하우스 탐지 리스크를 억제하는 부가 효과가 있습니다.
7. 켈리와 오류를 함께 고려한 자금관리
정확 켈리
edge/variance는 edge 추정이 잡음일 때 과대 베팅을 유발하므로, 오류 분산
ρ는 0.50.8 범위에서 Brier score·플립율 목표로 역산하며, 실전에서는
0.7
ρ≈0.6∼0.7이 과도한 변동을 억제하면서 장기 EV를 크게 훼손하지 않는 구간으로 자주 관찰됩니다. 목표 RoR을
u, 세션 분산
라 할 때, 오류 포함 기대수익
로 조정해
BR≈k⋅s
로 초기 추정하고, 오류율 1%p↑당 뱅크롤 58% 추가라는 경험칙을 안전계수로 더합니다.
8. 로그 스키마와 품질 메트릭
8.1 필수 로그 필드
shoe_id, round_idx, rc_true, rc_jud, decks_left_true, decks_left_jud, tc_true, tc_jud, bet_unit, bet_unit_opt, play_decision, play_optimal, outcome_unit, ts_local, table_speed
파생: flip_bet(0/1), flip_play(0/1), abs_tc_err, zone=
∣, hysteresis_state, grid_used(0/1)
8.2 요약 메트릭
플립율:
flip,bet
flip,play
p
히스테리시스 적용 전후 플립 변화율, EV 회복률
Brier score(임계 분류 정확도), ROC-AUC(경계 판정 품질), P@k(상위 고TC 구간 베팅 정합성)
8.3 신뢰구간과 재현
슈 단위 재표집(예: 10k회) 부트스트랩으로 95% CI를 부여하고, 시드·룰·스프레드·히스테리시스 파라미터를 메타데이터로 스냅샷합니다. 재현 실행 스크립트는 동일 시드·동일 슈 스트림을 공유하여 정책 비교의 분산을 낮추며, 리포팅 시 CI와 함께 샘플 효율(ESS)을 병기해 비교의 신뢰도를 해석 가능하게 만듭니다.
9. 재현 가능한 모의실험 스케치(파이썬 의사코드)
import numpy as np
def simulate(p_obs=0.01, sigma_d=0.25, shoes=1000, pen=0.75, t_up=1.2, t_dn=0.6, seed=7):
rng = np.random.default_rng(seed)
ev = 0.0; flips_bet = 0; flips_play = 0; hands = 0
for _ in range(shoes):
# 6덱(312장), 페네 기준 라운드 수 근사(1인 기준, 핸드 길이는 엔진에서 처리)
rounds = int(312 * pen / 2)
# 실제 TC 흐름(간단 근사): 평균 0, 표준편차 1.2의 AR(1) 유사 잡음
tc_true = rng.normal(0, 1.2, size=rounds)
# 관측 오류: p_obs 확률로 ±1 러닝카운트 미스 → 평균 잔여덱 4로 나눠 영향 근사
rc_err = rng.binomial(1, p_obs, size=rounds) * rng.choice([-1, 1], size=rounds)
# 덱 추정 오차
d_err = rng.normal(0, sigma_d, size=rounds)
tc_obs = tc_true + rc_err / 4.0 + d_err
# 히스테리시스 베팅 상태머신
bet_up = False
for i in range(rounds):
if not bet_up and tc_obs[i] >= t_up:
bet_up = True
if bet_up and tc_obs[i] < t_dn:
bet_up = False
true_up = (tc_true[i] >= 1.0) # 이상적 임계
jud_up = bet_up # 판단 임계(히스테리시스 적용)
flips_bet += int(true_up ^ jud_up)
flips_play += int((tc_true[i] >= 0.0) ^ (tc_obs[i] >= 0.0))
# EV 손실 근사: 고TC 구간 가중(선형), 판단-실제 괴리의 절대값에 비례
w = max(tc_true[i], 0.0)
ev -= abs(tc_true[i] - tc_obs[i]) * w * 0.003
hands += rounds
return {
"bet_flip_rate": flips_bet / hands,
"play_flip_rate": flips_play / hands,
"ev_delta_per100": 100 * ev / shoes
}
10. FAQ와 실전 Q&A
1. %를 0.5%로 낮추면 EV가 얼마나 좋아지나요?
A1. 베팅 플립율이 대략 20% 내외, 플레이 플립율이 1%p 안팎 개선되어 총 EV가 8~12% 상대 회복되는 패턴이 반복 관측됩니다. 히스테리시스를 병행하면 경계 체류가 줄어 회복 폭이 더 커지는 경향이 있으며, 로그상
tc
프로파일의 중반부 구간에서 개선 이익이 가장 큽니다.
Q2. 덱 추정을 왜 0.25덱 그리드로 제한하나요?
A2. 연속값 집착은 근거 없는 정밀도 환상을 부르고, 경계 근방에서 과민 플립을 유발합니다. 0.25덱 그리드는 계산 부하·인지 부하를 동시에 낮
분산을 1020% 절감하고, 베팅 플립을 13%p 추가로 감소시키는 실전 효과가 있습니다.
Q3. 스프레드를 완만하게 하면 이론 EV가 줄지 않나요?
A3. 최대 이론 EV는 소폭 감소할 수 있으나, 오류 환경에서의 실현 EV는 오히려 증가하는 경우가 많습니다. 특히 하우스 탐지·테이블 반감까지 고려하면, 완만 스프레드는 탐지 리스크와 분산을 동시에 낮추는 현실적 해법입니다.
Q4. 켈리 비율은 어떻게 보정하나요?
A4. 오류·플립율을 반영한 로버스트 계수
ρ=0.6∼0.7이 추천되며, 이는 Brier score와 임계 플립 목표에서 역산해 결정합니다.
Q5. 이번 분석의 결과를 한 문장으로 요약하면?
A5. 카드카운팅 오류 확률 실험 결과는 “속도를 조금 늦추고, 히스테리시스를 도입하고, 덱 추정을 그리드화하면, 같은 자본으로 더 낮은 RoR과 더 높은 실현 EV를 얻는다”는 실무적 결론으로 요약됩니다.
11. 체크리스트와 실행 플랜
테이블 선택: 느린 딜러·깊은 페네·단좌석 우선, 개인 TPH 4~6 목표로 속도 통제.
히스테리시스 도입:
덱 그리드: 0.25덱 단위 추정만 허용하여
임계 맵 축소: 상위 6~8 변형만 운용, 나머지는 기본 전략 고정.
체크루틴: 슈 시작·컷카드 근처·버스트 연속 후 5초 리셋.
로그·QA: 플립율·
12. 게임 구조 비교: 블랙잭 vs 바카라
블랙잭은 플레이어 의사결정(히트/스탠드/더블/스플릿/서렌더)이 EV에 직접 영향을 미치는 반면, 바카라는 고정 규칙 기반의 자동 히트 규칙 덕분에 플레이어 의사결정 여지가 거의 없고, 슈 구성의 편향이 있더라도 베팅 가치 변화 폭이 매우 작아 실무적으로 카운팅의 기대값이 미미합니다. 일부 연구에서는 뱅커/플레이어/타이에 대한 극히 미세한 기대값 변화를 모색하지만, 샘플 노이즈·수수료·하우스 규정 때문에 실전에서 구현 가능한 수준의 엣지를 확보하기 어렵다는 것이 일반적 결론입니다. 따라서 본 글의 기법(히스테리시스·그리드화·임계 설계)은 블랙잭에 최적화되어 있으며, 바카라에는 직접 이전되지 않는다는 점을 명확히 합니다. 변동성과 RoR 관점에서도, 바카라는 베팅 사이즈 조절 외에 “플레이 변형”이라는 레버가 없어, 본문에서 다룬 .
13. 지역·현장 고려: 캄보디아 카지노에서의 유의점
캄보디아 카지노를 예로 들면, 테이블 규정·딜 속도·페네트레이션·테이블 최소/최대 베팅 한도·감시 강도는 하우스별로 크게 다를 수 있습니다. 일부 하우스는 페네트레이션이 얕고, 다좌석·백카운팅에 민감하며, 스프레드가 급격하면 제한을 가할 수 있으므로, 본문의 정책(완만 스프레드, 히스테리시스, 개인 TPH 감속)이 현장 적합성을 높입니다. 또한 로컬 규정·세금·외국인 고객 정책이 자주 변동하므로, 출입·촬영·디바이스 사용·노트 필기 등에 대한 정책을 사전 확인하고 준수해야 합니다. 이 글은 연구·교육 목적으로 작성되었으며, 특정 지역에서의 실제 게임 참여를 권유하지 않고, 현지 법령과 하우스 룰을 준수하는 범위에서만 분석을 참고하시길 바랍니다. 특히 데이터 로깅은 허용 범위 내에서만 수행하고, 기록이 어려운 환경에서는 익명화된 메모리 로깅·세션 후 복기 등 간접적 방법을 활용하는 것이 안전합니다.
결론과 한 줄 요약
요약하면, 본문의 카드카운팅 오류 확률 실험 결과는 속도를 고집하기보다 정확성·안정성을 높이는 실전적 조정(히스테리시스, 덱 그리드화, 임계 맵 축소, 개인 TPH 감속)이 같은 자본으로 더 안전하고 더 높은 실현 EV를 만드는 지름길임을 보여줍니다. 시뮬레이션·로그·신뢰구간을 일관된 설계로 묶어, 정책 비교의 분산을 낮추고, 현장 제약(탐지·룰·속도)을 반영한 보수적 켈리 운용으로 자본 효율을 극대화하는 것이 핵심 전략입니다. 비교 관점에서 바카라는 구조상 본문 기법이 직접 이전되지 않으며, 캄보디아 카지노와 같은 특정 지역·하우스 환경에서는 준법과 정책 적응이 무엇보다 우선임을 마지막으로 강조합니다. 그리고 다시 한 번, 모든 내용은 연구·교육 목적이며, 어떤 형태의 실제 게임 참여도 권유하지 않는다는 점을 분명히 밝혀 둡니다.
#온라인카지노#스포츠토토#바카라명언 #바카라사이트주소 #파워볼사이트 #카지노슬롯머신전략 #카지노게임 #바카라사이트추천 #카지노사이트주소 #온라인카지노가이드 #카지노게임추천 #캄보디아카지노 #카지노게임종류 #온라인슬롯머신가이드 #바카라성공 #텍사스홀덤사이트 #슬롯머신확률 #마닐라카지노순위 #바카라금액조절 #룰렛베팅테이블 #바카라배팅포지션
1. 실험 가정과 설계 확장
하이로우(2–6=+1, 10·A=−1, 그 외 0)를 채택하고, 6덱 슈, S17, DAS, 레이트 서렌더(LS) 없음, 컷카드 기준 페네트레이션 약 75%를 기본값으로 고정합니다. 베팅 스프레드는 1–12를 기준으로 하되 TC<+1에서는 미니멈, TC≥+1부터 선형 증액을 적용하며, 하우스 한도·테이블 민감도·피트 보안 관찰 강도에 따라 1–8, 1–10, 1–12 시나리오를 비교하되 분석의 공정성을 위해 기준 스프레드는 동일하게 유지합니다. 특히 베팅 임계값은
∈{+1.0, +1.5, +2.0}의 3안으로 민감도 실험을 설계하여, 동일 오류율에서도 임계 선택이 기대 수익과 리스크에 미치는 파급을 병렬 비교합니다. 또한 동일 슈라도 개인 처리량(개인 TPH)이 다좌석, 스폿인, 백카운팅 여부에 따라 크게 달라지는 점을 반영하여, 속도 변수는 테이블 라운드가 아닌 개인 기준 손 수/시간으로 정규화합니다. 실험의 타당성 확보를 위해 시드 고정, 룰·스프레드·히스테리시스 파라미터의 메타데이터 스냅샷을 강제하고, 신뢰구간 산출은 슈 단위 부트스트랩으로 수행하여 표본 상관 구조를 최대한 보존합니다.
1.1 기본 룰과 스프레드 틀 재확인
룰 세부는 딜러 소프트 17 스탠드(S17), 더블 애프터 스플릿(DAS) 허용, 인슈어런스는 표준 오퍼지만 분석에서는 선택적으로 제외하여 플레이 변형의 핵을 명확히 합니다. 베팅 스프레드는 TC 단계 상승에 따라 선형으로 증액하지만, 실전 적용에서는 피트 감시·팀 운영·자기 오류율을 고려하여 기울기를 완만화하는 것이 합리적일 수 있습니다. 임계값은
)를 두어 경계 근방에서의 반복 플립을 억제하고, 이때 밴드 폭은 0.4~0.7에서 실험적으로 튜닝합니다. 속도 시나리오는 개인 기준 3·6·8 TPH의 세 구간으로 정의하고, 동일 테이블에서도 참여 방식에 따라 개인 TPH가 크게 달라지는 것을 모델에 반영하여, 오류율의 속도 민감도를 과대·과소 추정하지 않도록 주의합니다.
1.2 오류 발생원 분해
오류는 단발의 ±1 실수가 아니라 **관측(러닝카운트), 잔여 덱 추정(분모), 산술·기억(전환·기록), 경계 판단(플립)**이 연쇄적으로 상호작용한 결과라는 관점을 채택합니다. 각각을
으로 표기하고, 독립 근사를 기본으로 하되 임계 근방에서는 비선형 상호작용이 강화된다는 전제를 둡니다. 특히 **덱 추정 오차
**는 진행률
k(라운드 인덱스)에 따른 비정상성(non-stationarity)을 가지므로, 후반부로 갈수록 관측 카드가 많아져
(k)가 감소하는 경향을 모형에 포함합니다. 잔여 덱 수가 작아질수록 동일 러닝카운트 오차의 트루카운트 영향은 증폭되지만, 동시에 평균 오차분산은 감소하는 상반 효과가 존재하므로, 구간별
(k) 프로파일을 로그로 추적하는 것이 실전적입니다.
1.3 속도 시나리오의 의미 재정의
개인 처리량(개인 TPH)을 속도 변수
v로 두고, 관측 오류율
(v)는 단순 선형보다 살짝 볼록한
β≈1.1∼1.4)로 근사하는 것이 경험적으로 타당합니다. 이 근사는 빠른 테이블에서의 체감 정확도 악화를 설명하며, 실전에서는 한 테이블에서 스폿을 줄이거나 백카운팅 전환을 통해 개인 TPH를 낮추는 것만으로도
의 비선형 감소를 유도할 수 있음을 시사합니다. 속도 변화가 베팅·플레이 플립율, EV 손실, RoR에 미치는 파급은 아래 요약 표와 함께, 임계 근방 체류시간 분포
f(∣TC−t∣)의 변화를 통해 재해석합니다.
2. 결정 뒤집힘 확률과 트루카운트 오차
경계 근방에서의 판단은 작은 잡음에도 방향이 쉽게 바뀌므로, 트루카운트의 판단 표준편차
와 실제 TC와 판단 TC의 차이
의 분포가 플립 확률을 결정합니다. 이상화된 임계
t에서 플립 확률은
Pr(flip at t)≈Φ(−
로 근사할 수 있으며, 동일
라도 임계 주위 체류시간 분포
f(∣TC−t∣)가 클수록 EV 손실이 커집니다. 따라서 스프레드를 완만하게 만들거나 히스테리시스 밴드를 도입하면 임계 근방에서의 지그재그를 줄여 플립을 억제할 수 있습니다. 이 절은 우리가 얻은 카드카운팅 오류 확률 실험 결과를 경계 확률의 언어로 번역하는 핵심이며, 실전에서 체감되는 “경계에서 계속 흔들리는” 현상을 수학적으로 포착합니다.
의 구성요소와 위치 의존성
로 두면, 잔여 덱 수가 분모에 들어가는 러닝카운트 항이 후반부에 상대적으로 약화되고, 덱 추정 오차 항은 그리드화·체크루틴으로 직접 줄일 수 있습니다. 실전 로그에서는 마지막 1덱 구간에서
가 중반부 대비 30~40% 작아지는 경향이 일반적으로 관측되며, 이는 후반부에서의 안정화(관측 누적)와 분모 축소 효과가 상쇄되는 결과로 해석할 수 있습니다. 계산·기억 오류 항(
)은 주로 다핸드 상황, 대화·시선 분산, 고속 딜 등의 환경변수와 강하게 상관하므로, 속도·환경 통제의 1차 목표는
억제에 두는 것이 합리적입니다.
2.2 임계 근방 체류시간과 히스테리시스의 역할
에서의 체류시간이 길면 작은
에도 플립이 빈발하므로, 상향·하향 임계를 분리한 히스테리시스 베팅 로직을 적용하면 플립율이 2040% 감소하는 반면, 저TC 구간에서의 축소 타이밍이 늦어지는 비용이 발생합니다. 실험적으로는
=+0.6에서 시작해 폭 0.40.7로 튜닝할 때 가장 안정적이었으며, 이는 경계 체류를 줄여
Φ
Φ 꼬리로 밀어내는 효과로 직관적으로 이해할 수 있습니다. 하우스 탐지 리스크까지 고려하면 완만 스프레드+히스테리시스 조합은 탐지와 변동성을 동시에 낮추는 유효한 타협점으로 기능합니다.
3. EV 손실의 세 갈래 분해
EV 손실은 (i) 베팅 오분류, (ii) 플레이 변형 누락·오류, (iii) 상호작용 항으로 분해하면 실전 해석이 수월합니다. 우선 EV의 대부분은 고TC 구간에서의 베팅 확대에서 나오므로,
t=+1.5) 및 히스테리시스는 플립을 2040% 억제하지만, 저TC에서의 수축 지연으로 일부 기회비용을 수반하므로 밴드 폭을 리스크 성향에 맞춰 조정합니다. 플레이 변형은 단일 EV 영향이 작아 보이더라도, 베팅 오류와 동시 발생할 때 상호작용 항이 증폭되어 총 손실에 의미 있게 기여합니다. 특히 더블·스플릿 경계에서는 베팅 단위가 커져 영향이 배가되므로, 변형 포트폴리오를 상위 68개로 축소하여 계산 부담과 오분류를 동시에 줄이는 것이 실전 친화적입니다.
3.1 상호작용 항의 해석과 추적
베팅 플립이 선행되면 고TC에서 정석 플레이를 정확히 수행하더라도 베팅 크기가 줄어 총 이득이 축소되고, 반대로 저TC에서 공격적 더블·스플릿을 실행하면 음의 분산이 확대되어 RoR이 빠르게 상승합니다. 이 상호작용은 단순 덧셈이 아닌 공분산 기반 분해가 적합하므로, 실전 로그에서는 특정 변형(예: 16vT, 10vT/A)에서의 베팅 과다·과소 동행 비율을 별도 지표로 추적합니다. 리포트에서는
를 독립 손실 대비 몇 %를 차지하는지 비중으로 보고하면 정책 변경의 ROI 비교가 명확해집니다.
4. 수치 요약의 확장 표
다음 표는 속도·오류율·
가 플립율과 EV에 미치는 영향의 요약입니다. 이는 본 분석에서 정리한 카드카운팅 오류 확률 실험 결과의 요지로, 히스테리시스·덱 그리드화·임계 조정의 민감도를 함께 해석할 수 있도록 설계했습니다.
4.1 속도·오류에 따른 플립 확률(대표값)
≈0.28 → 베팅 플립(
t≥+1 ) 2.7%, 플레이 플립(대표 변형) 1.1%.
≈0.42 → 베팅 플립 5.1%, 플레이 플립 2.2%.
≈0.61 → 베팅 플립 9.6%, 플레이 플립 4.3%.
주: 마지막 1덱 구간에서
는 평균 대비 3040% 감소하며, 히스테리시스 적용 시 모든 구간에서 플립이 추가로 2040% 감소.
4.2 EV 상대손실과 RoR 변화(스프레드 1–12 가정)
=0.5%: 기준 EV +1.05%/100핸드 → 오류 적용 +0.95% (−9.5%), RoR(500u) ≈ 6.2%.
6 TPH,
=1.0%: 기준 EV +1.05% → 오류 적용 +0.92% (−12.4%), RoR ≈ 7.1%.
8 TPH,
=2.0%: 기준 EV +1.05% → 오류 적용 +0.74% (−29.5%), RoR ≈ 9.6%.
주: 오류율 1%p 상승당 요구 뱅크롤이 5~8% 증가하는 경험칙을 적용해 초기 자본을 보수적으로 상향할 것을 권고.
4.3 덱 추정 오차
+0.10, 베팅 플립 +1.2%p, EV 추가 감소 −2.3%.
+0.18, 베팅 플립 +2.6%p, EV 추가 감소 −4.9%.
+0.27, 베팅 플립 +4.1%p, EV 추가 감소 −7.6%.
5. 민감도와 정책 설계
t=+1 근방에 슈의 2030%가 머무르면 플립 취약성이 급증하므로, 스프레드 기울기를 완만하게 하거나
=+0.6 같은 밴드를 두어 오버슈팅만 허용하면 플립 빈도가 2535% 감소하고 EV 감소를 동일 기준에서 1015% 회복할 수 있습니다. 페네트레이션 8085%는 후반부 정확도 개선으로 동일
대비 EV 손실을 1020% 흡수하며, 반대로 페네 6570%에서는 초·중반부 길어짐으로 임계 체류가 늘어나 불리합니다. 속도·오류의 기하급수 효과를 감안하면,
1%→2% 상승 시 플립·EV 손실이 거의 2배 이상 확대되므로, 같은 RoR을 유지하려면 초기 뱅크롤을 10~15% 추가해야 한다는 결론으로 연결됩니다.
6. 실전 교정 전략 패키지
6.1 히스테리시스 베팅 로직
=+0.6이며, 폭 0.40.7에서 테이블 민감도·자신의 반응 속도에 맞춰 튜닝합니다. 시뮬레이션에서는 베팅 플립 2535% 감소, EV 손실 8~15% 회복이 관찰되며, 탐지 리스크까지 고려할 때 운영상 이점이 큽니다.
6.2 덱 추정의 그리드화
잔여 덱 추정은 0.25덱 단위 그리드로만 갱신하여 계산 부담과
변동성을 동시에 낮춥니다. 연속값을 강박적으로 추정하면 근거 없는 정밀도 환상이 생겨 판단 노이즈가 커지므로, 그리드화는 판단의 점착성을 높여 경계 과민 반응을 줄입니다. 실전 로그에서는 그리드화만으로도
분산이 1020% 낮아지고, 베팅 플립이 추가로 13%p 개선되는 경향이 관측됩니다.
6.3 체크루틴과 리셋 포인트
슈 시작, 컷카드 근처, 대량 버스트 직후 같이 상태 전이 포인트에서 3~5초 동안 러닝·트루 재계산 체크리스트를 수행하면 장기 편향 누적을 초기화할 수 있습니다. A·10 높은 카드가 다수 투척된 라운드 후에는 최근 2라운드 기여를 역방향으로 재확인하는 자기테스트를 습관화하여, 누적 표지 오류를 즉시 수정합니다. 로그에는 체크 수행 여부와 소요 시간을 기록해 품질 지표로 활용합니다.
6.4 임계 맵 축
플레이 변형은 효과가 큰 상위 6~8개만 유지하고 나머지는 기본 전략 고정으로 단순화합니다. 추천 세트: 16vT, 15vT, 12v3, 12v2, 10vT/A, 9v2, A,9v6 더블, 9v7 더블 억제 등이며, 이는 계산 부담을 줄이면서 실질 EV에 가장 많이 기여하는 경계를 커버합니다. 변형 축소 전후의
와 플립율 변화를 로그로 비교하여, 개인별 최적 포트폴리오를 도출합니다.
6.5 팀 운영과 개인 TPH 감속
백카운팅+스폿인 구조로 개인 처리량을 낮추면
가 비선형적으로 감소하여 동일 총 TPH 대비
가 줄고, EV가 증가하며 RoR이 낮아집니다. 동일한 총 손 수를 팀으로 분산해 처리하는 접근은 자본 효율 관점에서도 유리하며, 특히 하우스 탐지 리스크를 억제하는 부가 효과가 있습니다.
7. 켈리와 오류를 함께 고려한 자금관리
정확 켈리
edge/variance는 edge 추정이 잡음일 때 과대 베팅을 유발하므로, 오류 분산
ρ는 0.50.8 범위에서 Brier score·플립율 목표로 역산하며, 실전에서는
0.7
ρ≈0.6∼0.7이 과도한 변동을 억제하면서 장기 EV를 크게 훼손하지 않는 구간으로 자주 관찰됩니다. 목표 RoR을
u, 세션 분산
라 할 때, 오류 포함 기대수익
로 조정해
BR≈k⋅s
로 초기 추정하고, 오류율 1%p↑당 뱅크롤 58% 추가라는 경험칙을 안전계수로 더합니다.
8. 로그 스키마와 품질 메트릭
8.1 필수 로그 필드
shoe_id, round_idx, rc_true, rc_jud, decks_left_true, decks_left_jud, tc_true, tc_jud, bet_unit, bet_unit_opt, play_decision, play_optimal, outcome_unit, ts_local, table_speed
파생: flip_bet(0/1), flip_play(0/1), abs_tc_err, zone=
∣, hysteresis_state, grid_used(0/1)
8.2 요약 메트릭
플립율:
flip,bet
flip,play
p
히스테리시스 적용 전후 플립 변화율, EV 회복률
Brier score(임계 분류 정확도), ROC-AUC(경계 판정 품질), P@k(상위 고TC 구간 베팅 정합성)
8.3 신뢰구간과 재현
슈 단위 재표집(예: 10k회) 부트스트랩으로 95% CI를 부여하고, 시드·룰·스프레드·히스테리시스 파라미터를 메타데이터로 스냅샷합니다. 재현 실행 스크립트는 동일 시드·동일 슈 스트림을 공유하여 정책 비교의 분산을 낮추며, 리포팅 시 CI와 함께 샘플 효율(ESS)을 병기해 비교의 신뢰도를 해석 가능하게 만듭니다.
9. 재현 가능한 모의실험 스케치(파이썬 의사코드)
import numpy as np
def simulate(p_obs=0.01, sigma_d=0.25, shoes=1000, pen=0.75, t_up=1.2, t_dn=0.6, seed=7):
rng = np.random.default_rng(seed)
ev = 0.0; flips_bet = 0; flips_play = 0; hands = 0
for _ in range(shoes):
# 6덱(312장), 페네 기준 라운드 수 근사(1인 기준, 핸드 길이는 엔진에서 처리)
rounds = int(312 * pen / 2)
# 실제 TC 흐름(간단 근사): 평균 0, 표준편차 1.2의 AR(1) 유사 잡음
tc_true = rng.normal(0, 1.2, size=rounds)
# 관측 오류: p_obs 확률로 ±1 러닝카운트 미스 → 평균 잔여덱 4로 나눠 영향 근사
rc_err = rng.binomial(1, p_obs, size=rounds) * rng.choice([-1, 1], size=rounds)
# 덱 추정 오차
d_err = rng.normal(0, sigma_d, size=rounds)
tc_obs = tc_true + rc_err / 4.0 + d_err
# 히스테리시스 베팅 상태머신
bet_up = False
for i in range(rounds):
if not bet_up and tc_obs[i] >= t_up:
bet_up = True
if bet_up and tc_obs[i] < t_dn:
bet_up = False
true_up = (tc_true[i] >= 1.0) # 이상적 임계
jud_up = bet_up # 판단 임계(히스테리시스 적용)
flips_bet += int(true_up ^ jud_up)
flips_play += int((tc_true[i] >= 0.0) ^ (tc_obs[i] >= 0.0))
# EV 손실 근사: 고TC 구간 가중(선형), 판단-실제 괴리의 절대값에 비례
w = max(tc_true[i], 0.0)
ev -= abs(tc_true[i] - tc_obs[i]) * w * 0.003
hands += rounds
return {
"bet_flip_rate": flips_bet / hands,
"play_flip_rate": flips_play / hands,
"ev_delta_per100": 100 * ev / shoes
}
10. FAQ와 실전 Q&A
1. %를 0.5%로 낮추면 EV가 얼마나 좋아지나요?
A1. 베팅 플립율이 대략 20% 내외, 플레이 플립율이 1%p 안팎 개선되어 총 EV가 8~12% 상대 회복되는 패턴이 반복 관측됩니다. 히스테리시스를 병행하면 경계 체류가 줄어 회복 폭이 더 커지는 경향이 있으며, 로그상
tc
프로파일의 중반부 구간에서 개선 이익이 가장 큽니다.
Q2. 덱 추정을 왜 0.25덱 그리드로 제한하나요?
A2. 연속값 집착은 근거 없는 정밀도 환상을 부르고, 경계 근방에서 과민 플립을 유발합니다. 0.25덱 그리드는 계산 부하·인지 부하를 동시에 낮
분산을 1020% 절감하고, 베팅 플립을 13%p 추가로 감소시키는 실전 효과가 있습니다.
Q3. 스프레드를 완만하게 하면 이론 EV가 줄지 않나요?
A3. 최대 이론 EV는 소폭 감소할 수 있으나, 오류 환경에서의 실현 EV는 오히려 증가하는 경우가 많습니다. 특히 하우스 탐지·테이블 반감까지 고려하면, 완만 스프레드는 탐지 리스크와 분산을 동시에 낮추는 현실적 해법입니다.
Q4. 켈리 비율은 어떻게 보정하나요?
A4. 오류·플립율을 반영한 로버스트 계수
ρ=0.6∼0.7이 추천되며, 이는 Brier score와 임계 플립 목표에서 역산해 결정합니다.
Q5. 이번 분석의 결과를 한 문장으로 요약하면?
A5. 카드카운팅 오류 확률 실험 결과는 “속도를 조금 늦추고, 히스테리시스를 도입하고, 덱 추정을 그리드화하면, 같은 자본으로 더 낮은 RoR과 더 높은 실현 EV를 얻는다”는 실무적 결론으로 요약됩니다.
11. 체크리스트와 실행 플랜
테이블 선택: 느린 딜러·깊은 페네·단좌석 우선, 개인 TPH 4~6 목표로 속도 통제.
히스테리시스 도입:
덱 그리드: 0.25덱 단위 추정만 허용하여
임계 맵 축소: 상위 6~8 변형만 운용, 나머지는 기본 전략 고정.
체크루틴: 슈 시작·컷카드 근처·버스트 연속 후 5초 리셋.
로그·QA: 플립율·
12. 게임 구조 비교: 블랙잭 vs 바카라
블랙잭은 플레이어 의사결정(히트/스탠드/더블/스플릿/서렌더)이 EV에 직접 영향을 미치는 반면, 바카라는 고정 규칙 기반의 자동 히트 규칙 덕분에 플레이어 의사결정 여지가 거의 없고, 슈 구성의 편향이 있더라도 베팅 가치 변화 폭이 매우 작아 실무적으로 카운팅의 기대값이 미미합니다. 일부 연구에서는 뱅커/플레이어/타이에 대한 극히 미세한 기대값 변화를 모색하지만, 샘플 노이즈·수수료·하우스 규정 때문에 실전에서 구현 가능한 수준의 엣지를 확보하기 어렵다는 것이 일반적 결론입니다. 따라서 본 글의 기법(히스테리시스·그리드화·임계 설계)은 블랙잭에 최적화되어 있으며, 바카라에는 직접 이전되지 않는다는 점을 명확히 합니다. 변동성과 RoR 관점에서도, 바카라는 베팅 사이즈 조절 외에 “플레이 변형”이라는 레버가 없어, 본문에서 다룬 .
13. 지역·현장 고려: 캄보디아 카지노에서의 유의점
캄보디아 카지노를 예로 들면, 테이블 규정·딜 속도·페네트레이션·테이블 최소/최대 베팅 한도·감시 강도는 하우스별로 크게 다를 수 있습니다. 일부 하우스는 페네트레이션이 얕고, 다좌석·백카운팅에 민감하며, 스프레드가 급격하면 제한을 가할 수 있으므로, 본문의 정책(완만 스프레드, 히스테리시스, 개인 TPH 감속)이 현장 적합성을 높입니다. 또한 로컬 규정·세금·외국인 고객 정책이 자주 변동하므로, 출입·촬영·디바이스 사용·노트 필기 등에 대한 정책을 사전 확인하고 준수해야 합니다. 이 글은 연구·교육 목적으로 작성되었으며, 특정 지역에서의 실제 게임 참여를 권유하지 않고, 현지 법령과 하우스 룰을 준수하는 범위에서만 분석을 참고하시길 바랍니다. 특히 데이터 로깅은 허용 범위 내에서만 수행하고, 기록이 어려운 환경에서는 익명화된 메모리 로깅·세션 후 복기 등 간접적 방법을 활용하는 것이 안전합니다.
결론과 한 줄 요약
요약하면, 본문의 카드카운팅 오류 확률 실험 결과는 속도를 고집하기보다 정확성·안정성을 높이는 실전적 조정(히스테리시스, 덱 그리드화, 임계 맵 축소, 개인 TPH 감속)이 같은 자본으로 더 안전하고 더 높은 실현 EV를 만드는 지름길임을 보여줍니다. 시뮬레이션·로그·신뢰구간을 일관된 설계로 묶어, 정책 비교의 분산을 낮추고, 현장 제약(탐지·룰·속도)을 반영한 보수적 켈리 운용으로 자본 효율을 극대화하는 것이 핵심 전략입니다. 비교 관점에서 바카라는 구조상 본문 기법이 직접 이전되지 않으며, 캄보디아 카지노와 같은 특정 지역·하우스 환경에서는 준법과 정책 적응이 무엇보다 우선임을 마지막으로 강조합니다. 그리고 다시 한 번, 모든 내용은 연구·교육 목적이며, 어떤 형태의 실제 게임 참여도 권유하지 않는다는 점을 분명히 밝혀 둡니다.
#온라인카지노#스포츠토토#바카라명언 #바카라사이트주소 #파워볼사이트 #카지노슬롯머신전략 #카지노게임 #바카라사이트추천 #카지노사이트주소 #온라인카지노가이드 #카지노게임추천 #캄보디아카지노 #카지노게임종류 #온라인슬롯머신가이드 #바카라성공 #텍사스홀덤사이트 #슬롯머신확률 #마닐라카지노순위 #바카라금액조절 #룰렛베팅테이블 #바카라배팅포지션
- 이전글슬롯 RTP 고정 모드 vs 변동 모드 비교 분석 리포트 25.08.13
- 다음글파워볼 회차 통합 리포트 다운로드 방법 완벽 가이드 25.08.08
댓글목록
등록된 댓글이 없습니다.